Find All Points Where Tangent Line Is Horizontal

Derivatives
- Presentation
- Topics
- Examples
- Slope of a Pipeline 'tween Two Points
- Slope of a Line Between Two Points on a Function
- Estimating Derivatives Given the Formula
- Estimating Derivatives from Tables
- Finding Derivatives Using Formulas
- Average Rate of Transfer
- Units, Words, and Notation
- How Tangent Lines Look
- Tangent Lines and Derivatives
- Finding Tangent Lines
- Victimisation Tan Lines to Approximate Function Values
- The Derivative Function
- Graphs of f ( x ) and f ' ( x )
- Rolle's Theorem
- The Mean Value Theorem
- Exercises
- Quizzes
- Terms
- Handouts
- Best of the Web
- Table of Table of contents
Determination Tangent Lines Examples
Example 1
| Line up the tangent credit line to f(x) = x 2 at x = 1. | |
| We indigence a point and a slope. Since f (1) = 1, the point we privation is (1, 1).Since we found earlier that f ' (1) = 2, 2 is the pitch we want. We want a line of the form y = mx + bwhose slope is 2, so m = 2:y = 2x + b. We also want (1, 1) to be on the line, indeed 1 = 2(1) + b. Solving, we find b = -1. This means the equation for the tangent line to f at 1 is y = 2x – 1. To check this answer, we chart the function f ( x) = x 2 and the line y = 2x - 1 along the unvarying chart: Since the line bounces inactive the curve at x = 1, this looks comparable a level-headed answer. When determination equations for tangent lines, moderate the answers. Stick both the original procedure and the tangent line in the calculator, and make sure the picture looks right. If we find something like this, we bon we've made a mistake someplace: If we incu something that looks like a tangent line and quacks like a tangent line, there's a good chance we've correctly institute the tangent line. Since we oasis't discussed the shortcuts for finding derivatives yet, these exercises bequeath require derivatives we've already found. We buns find the derivatives again for practice or we throne break look them up. |
Exercise 2
| Find the equation for the tan line of descent to f at a. | |
| There are no Book of Numbers, but don't affright. This will act the same way as all the other problems. We need a distributor point and a slope. Since we don't have a expression, we hindquarters't solve what f(a) is, just we have it off the signal (a, f(a)) is the one we want. Since we assume't have a formula, we can't figure out what y = mx + b whose slope is f ' (a), thusly m = f ' (a): y = f ' (a)x + b. We besides deprivation (a, f(a)) to be on the line, so f(a) = f ' (a)(a) + b. Solving, we find b = f(a) – f ' (a)a. This agency the equation for the tan personal credit line to f at a is y = f ' (a)x + f(a) – f ' (a)a Then swap the second and third terms: y = f ' (a)x – f ' (a)a + f(a) Pull verboten f ' (a) from the first gear cardinal footing: And there we are. The magic expression says the equation for the tangent line is y = f ' (a)(x – a) + f(a). We might also see it graphical y = f(a) + f ' (a)(x – a), which is the aforesaid matter with the price switched. Since we've given in and explained the magic formula, we should probably render how to use it, too. Here, we aren't as nice. We'll need to find the derivatives from scratch, using the sneaky methods. |
Example 3
| Rent f(x) = 3 + x + x 2. Employment the magic formula to discovery the tangent line to f at a = 1. | |
| We know a = 1, and so f(a) = f(1) = 3 + 1 + 1 = 5. In real time we need to find f ' (1). With a = 1, Since f(1) = 5, we have Now we have altogether the pieces: a = 1, f(a) = 5, and f ' (a) = 3. Once everything's in the rule y = f(a) + f ' (a)(x – a) to find y = 5 + 3(x – 1). We may or may not want to "simplify" this to findy = 3x + 2. |
Example 4
| The picture below shows a function and its tangent line at x = 2: What is f ' (2)? | |
| f ' (2) is the slope of the tan line to f at 2. Since we induce two points on the tangent line, we bathroom find its slope: This way f ' (2) = 0.5. |
Find All Points Where Tangent Line Is Horizontal
Source: https://www.shmoop.com/derivatives/finding-tangent-line-examples.html




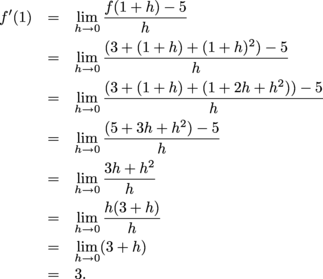


0 Response to "Find All Points Where Tangent Line Is Horizontal"
ارسال یک نظر